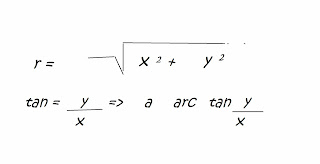teori :: Matematika ..: 2013

Kamis, 19 September 2013

Aturan Cosinus ...

* Aturan Cosinus
Cirinya = ^memiliki dua sisi dan satu sudut ..
Rumus ::::::

Selasa, 17 September 2013

Aturan Sinus ...

* Aturan Sinus

Ciri :::

- Dua sudut satu sisi

- Sudut itu ditandai dengan huruf Besar

- Sisi itu ditandai dengan huruf kecil

Memakai rumus harus 2 ,, tidak boleh 1 ..

Koordinat Kutub (Polar)

Koordinat Kutub adalah letak suatu titik yang disajikan dalam bentuk r dan α.
α. berbentuk derajat (α') ..

Rumus untuk merubah Koordinat Kutup (polar) kedalam Koordinat Cartesius ..

arc => Kebalikan

a berbentuk derajat (a')

Jumat, 13 September 2013

Sudut Trigonometri ..

Agar dapat cepat hafal ,, hafalkan saja SIN , TAN , dan SEC .. Karna COS merupakan kebalikan dari SIN , COT merupakan kebalikan dari TAN , dan COSEC merupakan kebalikan dari SEC .. :)

Ket = ( | ) adalah akar

#Semoga Membantu ...

Dalam matematika, Sistem koordinat Kartesius digunakan untuk menentukan tiap titik dalam bidang dengan menggunakan dua bilangan yang biasa disebut koordinat x dan koordinat y dari titik tersebut.
Untuk mendefinisikan koordinat diperlukan dua garis berarah yang tegak lurus satu sama lain (sumbu x dan sumbu y), dan panjang unit, yang dibuat tanda-tanda pada kedua sumbu tersebut
Istilah Kartesius digunakan untuk mengenang ahli matematika sekaligus filsuf dari Perancis Descartes, yang perannya besar dalam menggabungkan aljabar dan geometri (Cartesius adalah latinisasi untuk Descartes). Hasil kerjanya sangat berpengaruh dalam perkembangan geometri analitik, kalkulus, dan kartografi .

Koordinat Cartesius ...

Rumusnya merubah Koordinat Cartesius kedalam Koordinat Kutub (Polar) ..

Perbandingan Trigonometri Sudut Berelasi ..

I. Semua Positif

II. Hanya Sin saja yang Positif

III. Hanya Tan saja yang Positif

VI. Hanya Cos saja yang Positif

Jika terletak pada sudut 90' - 270' (garis tegak) harus dibalik
Jika terletak pada sudut 180' - 360' (garis mendatar) tetap atau tidak harus dibalik
Kalau lebih dari 360' kembali keletak kuadrat I.

Relasi 90-a
sin (90-a) =        cos
cos (90-a) =         sin
tan (90-a) =          cot
cot (90-a) =          tan
sec (90-a) =         cosec
cosec (90-a) =      sec
Relasi 90+a
sin (90+a) =       cos
cos (90+a) =      sin
tan (90+a)=       -cot
cot (90+a)=        -tan
sec   (90+a)=      -cosec
cosec (90+a)=   -sec
{ Karna Relasi ini terletak disudut 90-270 (tegak lurus) maka harus dibalik ,, dan terletak dikuadrat II maka hanya sin saja yg POSITIF , sedangkan yg lain NEGATIF }
Relasi 180-a
sin (180-a) =         sin
cos (180-a) =        -cos
tan (180-a) =         -tan
cot (180-a) =         -cot
sec (180-a) =         -sec
cosec (180-a) =     -cosec
{ Karna Relasi ini terletak disudut 180-360 (medatar) maka tetap atau tidak dibalik ,, dan terletak di kuadrat II maka hanya SIN saja yang POSITIF , sedangkan yang lain NEGATIF }
Relasi 180+a
sin (180+a) =         -sin
cos (180+a) =        -cos
tan (180+a) =         tan
cot (180+a) =         cot
sec (180+a) =       -sec
cosec (180+a) =     -cosec
{ Karna Relasi ini terletak disudut 180-360 (mendatar) maka tetap atau tidak dibalik ,, dan terletak di kuadrat III maka hanya TAN saja yang POSITIF , sedangkan yang lain NEGATIF }
Relasi 270-a
sin (270-a) =             -cos
cos (270-a) =            -sin
tan (270-a) =             cot
cot (270-a) =             tan
sec (270-a) =             -cosec
cosec (270-a) =         -sec
{ Karna Relasi ini terletak disudut 90-270 (tegak lurus) maka harus dibalik ,, dan terletakk dikuadrat III maka hanya TAN saja yang POSITIF , sedangkan yang lain NEGATIF }
Relasi 270+a
sin (270+a) =             -cos
cos (270+a) =            sin
tan (270+a) =             -cot
cot (270+a) =             -tan
sec (270+a) =             cosec
cosec (270+a) =         -sec
{ Karna Relasi ini terletak disudut 90-270 (tegak lurus) maka harus dibalik ,, dan terletakk dikuadrat IV maka hanya COS saja yang POSITIF , sedangkan yang lain NEGATIF }
Relasi (n.360-a)
sin (n.360-a) =            -sin
cos (n.360-a) =            cos
tan (n.360-a) =            -tan
cot (n.360-a) =             -cot
sec (n.360-a) =            sec
cosec (n.360-a) =        -cosec
{ Karna Relasi ini terletak disudut 180-360 (mendatar) maka tetap atau tidak dibalik ,, dan terletak di kuadrat dan terletakk dikuadrat IV maka hanya COS saja yang POSITIF , sedangkan yang lain NEGATIF }
Relasi (n.360+a)
sin (n.360+a) =            sin
cos (n.360+a) =           cos
tan (n.360+a) =            tan
cot (n.360+a) =            cot
sec (n.360+a) =            sec
cosec (n.360+a) =        cosec
{ Karna Relasi ini terletak disudut 180-360 (mendatar) maka tetap atau tidak dibalik ,, dan melebihi 360' kembali ke kuadrat I ,, dikuadrat I semuanya POSITIF }

Kt = n sama dengan 1(satu)

#Semoga Membantu . :)

Senin, 02 September 2013

Perbandingan Trigonometri ...

ket :: - mi (miring)
- de (depan)
- sa (samping)

sinus (sin) = de/mi
cosinus (cos) = sa/mi
tangen (tan) = de/mi
cotangen (cot) = sa/de
secan (sec) = mi/sa
cosecan (cosec) = mi/de

Ukuran Sudut Dalam Radian ..

Rumusnya .. !!
1' = য় /180' radian

1 radian = 180'/য়

example ;;;

1. 30'

jawab .. 30 x য় /180' = 1/6 য় radian

2. 2/3 য় radian

jawab ... 2/3 য় radian = 2/~~3 য়~~ x ~~180~~/য় = 2 x 60 = 120'

Pengertian Trigonometri ...

Trigonometri (dari bahasa Yunani trigonon = tiga sudut dan metro = mengukur) adalah sebuah cabang matematika yang berhadapan dengan sudut segitiga dan fungsi trigonometrik seperti sinus, cosinus, dan tangen. Trigonometri memiliki hubungan dengan geometri, meskipun ada ketidaksetujuan tentang apa hubungannya; bagi beberapa orang, trigonometri adalah bagian dari geometri.

Pengertian dan definisi Trigonometri. Trigonometri adalah bagian dari ilmu matematika yang mempelajari relasi antara sudut dan sisi sebuah segitiga. Trigonometri adalah suatu konsep dalam matematika yang memungkinkan kita menghitung dan memperoleh nilai dari suatu benda tanpa kita perlu melakukan pengukuran secara manual. Trigonometri sangat penting dalam kehidupan kita. sebagian besar pengukuran yang tidak bisa dilakukan secara manual dapat di lakukan dengan menggunakan konsep dan fungsi trigonometri. - See more at: http://www.kamuslife.com/2013/01/pengertian-dan-definisi-trigonometri.html#sthash.aYFzzhe1.dpuf